RPACT Training for FGK

Gernot Wassmer

July 22, 2025

Welcome to the RPACT Training 2025!

This website is accessible at fgk.rpact.com


Overview

  • Interim Analyse ohne Fallzahlanpassung
  • Interim Analyse mit verblindeter Fallzahlanpassung
  • Fallzahlanpassung basierend auf entblindeter Varianz
  • Multi-arm trials
  • Herleitung von Schätzern und Konfidenzintervallen
  • Praktische Beispiele für:
    • Cochran-Mantel-Haenszel Test: Common Odds Ratio inklusive Konfidenzintervall
    • Lineares Model: LS-Means mit Konfidenzintervall und Konfidenzintervall der Differenz

Questions and Answers

Interim Analyse ohne Fallzahlanpassung

  • Überprüfung der Safety (z.B. AEs), keine weiteren Anpassungen

    • Wird dies als Fixed Design bezeichnet? Oder ist die Bezeichnung egal?

      Design mit safety monitoring

    • Muss etwas bei der Studienplanung berücksichtigt werden?

      Organisation eines DSMBs (charter, etc.)

Interim Analyse ohne Fallzahlanpassung

  • Non-binding futility, kein Test auf Efficacy:

    • Nennt man das bereits gruppensequentielles Design?

      Ja, es ist ein gruppensequentielles Design, da eine IA geplant ist.

    • Dürfte so eine Studie wie ein Fixed Design geplant werden? Oder muss die IA berücksichtigt werden, bezahlt man in irgendeiner Form dafür (z.B. Power)?

      Bei Planung sollte futility stop berücksichtigt werden (power!)

    • Wenn der p-Wert für die Futility Entscheidung verwendet wird (also z.B. Stop für Futility für p > 0.9), muss bei der finalen Analyse dafür adjustiert werden?

      Nein bei non-binding futility, man kann bei binding futility.

Interim Analyse ohne Fallzahlanpassung

  • Non-binding futility, Test auf Efficacy:

    • Alpha-spending: theoretisch darf man den Zeitpunkt und die Anzahl an Zwischenauswertungen anpassen. Wird es von Behörden akzeptiert, Anzahl und Zeitpunkt der Zwischenauswertung nicht im Protokoll zu präspezifizieren?

      Bei Verwendung des alpha spending Ansatzes sollte Zeitpunkt spezifiziert werden, information bei IA ist flexibel. Zeitpunkt darf nicht (datanabhängig) angepasst werden, wenn alpha spending verwendet wird.

    • Welchen Mehrwert hat es einen Test auf Efficacy einzubauen, wenn die Chance für einen Abbruch bei der IA minimal ist (z.B. mit O‘Brien Fleming Design)? Gibt es einen sinnvollen Anwendungsfall bzw. welche Daseinsberechtigung hat ein O‘Brien Fleming Design?

      O’Brien Fleming design ist sehr etablierte Methode, die von Behörden akzeptiert wird. Für minimale Abruchchance mit minimalen Kosten verbaut man sich nichts!

Interim Analyse mit verblindeter Fallzahlanpassung

  • Kein Test auf Futility/Efficacy:

    • „Bezahlt“ man für so eine Analyse? Man kann gepoolt auswerten und hat kein alpha Adjustment.

      Type I error rate inflation muss diskutiert werden

    • Nachteile:

      • Fallzahlneuberechnung kann irreführend sein
      • Bräuchte es ein IDMC?
      • Gibt es weitere Nachteile?

      Wann irreführend? IDMC ist nicht notwendig, da keine Entscheidung getroffen wird

    • Müsste ein Check auf Futility (non-binding) in irgendeiner Form bei der Auswertung berücksichtigt werden?

      Verblindete Fallzahlanpassung und futility check schließen sich aus

Fallzahlanpassung basierend auf entblindeter Varianz

  • Kein Test auf Efficacy, ggf. auch Check auf Futility:

    • Dürfen bei einigermaßen großer Fallzahl die Daten gepoolt und ohne alpha Adjustment ausgewertet werden? Gibt es eine Daumenregel?

      Definitiv nein, ich weiß ja nicht, wie die große Fallzahl entstanden ist!

  • Test auf Efficacy, ggf. auch Check auf Futility:

    • Dürfen die Daten gepoolt ausgewertet werden?

      Promizing zone approach: wenn bedingte power > 50% kann Fallzahl erhöht und gepoolt ausgewertet werden

    • Ist ein alpha Adjustment für den Efficacy Test ausreichend oder ist eine weitere Adjustierung aufgrund der Fallzahlanpassung notwendig?

      Weitere Anpassung i.A. nötig

Multi-arm trials

  • 3-armige Studie mit zwei Dosisgruppen; es wird nur die bessere Verumgruppe nach der IA weitergeführt:

    • Muss die finale Auswertung mit der inversen Normalmethode erfolgen?

      Nicht muss, aber gute Anwendung. Bei festen Selektionsregeln gibt es andere Verfahren, die aber m.E. wenig Vorteile bringen

    • Ohne Test auf Efficacy bei der IA: ist eine alpha Adjustierung für die IA notwendig?

      Bitte diese Frage näher spezifizieren

Allgemeines

  • Wie wirkt es sich aus, wenn wir kein superiority sondern ein non-inferiority trial haben?

    Bitte auch diese Frage näher spezifizieren

Herleitung von Schätzern und Konfidenzintervallen

  • Allgemeine Einführung welche Punkt-Schätzer es gibt und was man berücksichtigen muss
  • Wie werden Konfidenzintervalle für die Punktschätzer hergeleitet?
  • Praktische Beispiele für:
    • Cochran-Mantel-Haenszel Test: Common Odds Ratio inklusive Konfidenzintervall
    • Lineares Model: LS-Means mit Konfidenzintervall und Konfidenzintervall der Differenz

Vorschläge für Erweiterungen in rpact

  • Cochran-Mantel-Haenszel Test (Auswertung und Fallzahlanpassung mit Common Odds Ratio)
  • Wilcoxon Rangsummentest (Auswertung und Fallzahlanpassung)

Estimation and p-Values in Group Sequential Designs

  • p-values:
    • stagewise \(p\)-values
    • Cumulative \(p\)-values
    • Final analysis adjusted (“exact”) \(p\)-values
    • Repeated \(p\,\)-values
  • Estimation:
    • Unadjusted CIs
    • Final analysis adjusted (“exact”) CIs based on stagewise ordering
    • Repeated Confidence Intervals (RCIs)
    • Point estimates

Exact p-values: Ordering of sample space

  • In a fixed-sample design, a \(p\)-value is defined as

    \[p = P_{H_0}(Z \geq z)\;.\]

  • In a group sequential design, define overall \(p\)-value at the end of the trial through

    \[p_\text{final} = P_{H_0}\big((Z^*_{\cal K}, {\cal K}) \succeq (z^*_k,k)\big)\;.\]

Needs ordering of the sample space

Focus on methods based on stagewise ordering of group-sequential sample space:

  • Good theoretical properties
  • Available in software (rpact, EaSt, etc.)

Example four-stage design, two-sided test

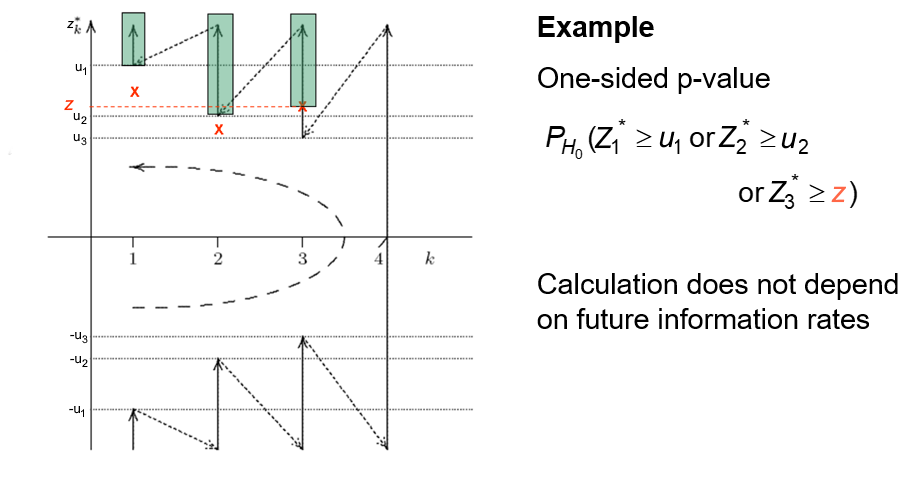
This \(p\)-value can only be calculated once, at the end of the trial

Overall repeated p-values

  • The overall repeated \(p\,\)-value is the smallest significance level for which \(H_0\) can be rejected at stage \(k\) with the given data.
  • Repeated \(p\,\)-values can be calculated at any stage of the trial.
  • Repeated \(p\,\)-values exactly correspond to the test decision.
  • Under \(H_0\), distribution of repeated \(p\,\)-value stochastically larger than uniform.
  • Repeated \(p\,\)-values are conservative.

Confidence intervals and estimates

Confidence intervals:

  • Repeated confidence intervals: sequence of intervals \(I_k\) for which

\[ P_\delta(\delta \in I_k \text{ for all } k = 1,\ldots,K) \geq 1 - \alpha \]

  • Final analysis adjusted confidence interval, calculated by:

\[ P_{\delta^L}\big((Z^*_{\cal K}, {\cal K}) \succeq (z^*_k,k)\big) = \alpha/2 \text{ and } P_{\delta^U}\big((Z^*_{\cal K}, {\cal K}) \preceq (z^*_k,k)\big) = \alpha/2 \]


Point estimates:

  • Median unbiased estimator: Upper limit of a one-sided 50% confidence interval of the form \((-\infty; \delta_{0.5}]\).

  • Mid-point of RCI

Group Sequential and Adaptive Analysis with rpact

Analysing a Trial with Interim Stages Using rpact

  • Group sequential test
  • Inverse normal combination test
  • Fisher’s combination test
  • Repeated confidence intervals, p-Values
  • Final analysis adjusted confidence intervals, p-Values
  • Conditional Rejection Probability (Müller & Schäfer)
  • Conditional power assessment
  • All this for continuous, binary, and survival endpoint

Group Sequential and Adaptive Analysis

getAnalysisResults(design, dataInput,...)

design The trial design.

dataInput The summary data used for calculating the test results. This is either an element of DataSetMeans, of DataSetRates, or of DataSetSurvival.


Given a design and a dataset, at given stage the function calculates the test results (effect sizes, stage-wise test statistics and p-values, overall p-values and test statistics, conditional rejection probability (CRP), conditional power, Repeated Confidence Intervals (RCIs), repeated overall p-values, and final stage p-values, median unbiased effect estimates, and confidence intervals.)

The conditional power is calculated only if (at least) the sample size for the subsequent stage(s) is specified. Median unbiased effect estimates and confidence intervals are calculated only if a group sequential or an inverse normal design was chosen. A final stage \(p\)-value for Fisher’s combination test is calculated only if a two-stage design was chosen.

Group Sequential and Adaptive Analysis

dataInput

  • An element of DataSetMeans for one sample is created by

    getDataset(means =, stDevs =, sampleSizes =)

    where means, stDevs, sampleSizes are vectors with stagewise means, standard deviations, and sample sizes of length given by the number of available stages.

  • An element of DataSetMeans for two samples is created by

    getDataset(means1 =, means2 =, stDevs1 =, stDevs2 =, sampleSizes1 =, sampleSizes2 =)

    where means1, means2, stDevs1, stDevs2, sampleSizes1, sampleSizes2 are vectors with stagewise means, standard deviations, and sample sizes for the two treatment groups of length given by the number of available stages.

Use of cumMeans, cumulativeMeans, overallMeans, cumStDevs, cumulativeStDevs, overallStDevs, n, cumN, etc., is also possible

Group Sequential and Adaptive Analysis

dataInput

  • An element of DataSetMeans for G + 1 samples is created by

    getDataset(means1 =,..., means[G+1] =, stDevs1 =, ..., stDevs[G+1] =, sampleSizes1 =, ..., sampleSizes[G+1] =),

    where means1, ..., means[G+1], stDevs1, ..., stDevs[G+1], sampleSizes1, ..., sampleSizes[G+1] are vectors with stagewise means, standard deviations, and sample sizes for G+1 treatment groups of length given by the number of available stages.

  • Last treatment arm G + 1 always refers to the control group that cannot be deselected.

  • Only for the first stage all treatment arms needs to be specified, so treatment arm selection with an arbitrary number of treatment arms for subsequent stage can be considered.

  • Analogue definition of DataSetRates and DataSetSurvival.

Example

Define the design:

library(rpact)

designIN <- getDesignInverseNormal(
  kMax = 4,
  typeOfDesign = "WT", 
  deltaWT = 0.45
)

Data summary for binary data:

dataExample <- getDataset(
  n1      = c( 8, 10,  9),
  n2      = c(11, 13, 12),
  events1 = c( 3,  4,  5),
  events2 = c( 8, 10, 12)
)

Analysis results

getAnalysisResults(
  design = designIN,
  dataInput = dataExample, 
  directionUpper = FALSE
) |> summary()

Analysis results for a binary endpoint

Sequential analysis with 4 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a two-sample test for rates, normal approximation test. H0: pi(1) - pi(2) = 0 against H1: pi(1) - pi(2) < 0.

Stage 1 2 3 4
Fixed weight 0.5 0.5 0.5 0.5
Cumulative alpha spent 0.0070 0.0138 0.0198 0.0250
Stage levels (one-sided) 0.0070 0.0088 0.0100 0.0110
Efficacy boundary (z-value scale) 2.456 2.372 2.325 2.291
Cumulative effect size -0.352 -0.361 -0.389
Cumulative treatment rate 0.375 0.389 0.444
Cumulative control rate 0.727 0.750 0.833
Stage-wise test statistic -1.536 -1.799 -2.567
Stage-wise p-value 0.0623 0.0360 0.0051
Inverse normal combination 1.536 2.358 3.407
Test action continue continue reject and stop
Conditional rejection probability 0.0777 0.3093 0.9062
95% repeated confidence interval [-0.739; 0.197] [-0.646; 0.002] [-0.618; -0.140]
Repeated p-value 0.1561 0.0259 0.0009
Final p-value 0.0139
Final confidence interval [-0.598; -0.039]
Median unbiased estimate -0.333

Check repeated p-value

getAnalysisResults(
  design = getDesignInverseNormal(
      kMax = 4,
      alpha = 0.02595,    
      typeOfDesign = "WT", 
      deltaWT = 0.45
    ),
  dataInput = dataExample, 
  directionUpper = FALSE
) |> summary()

Analysis results for a binary endpoint

Sequential analysis with 4 looks (inverse normal combination test design), one-sided overall significance level 2.6%. The results were calculated using a two-sample test for rates, normal approximation test. H0: pi(1) - pi(2) = 0 against H1: pi(1) - pi(2) < 0.

Stage 1 2 3 4
Fixed weight 0.5 0.5 0.5 0.5
Cumulative alpha spent 0.0073 0.0144 0.0206 0.0260
Stage levels (one-sided) 0.0073 0.0092 0.0104 0.0114
Efficacy boundary (z-value scale) 2.440 2.357 2.310 2.277
Cumulative effect size -0.352 -0.361 -0.389
Cumulative treatment rate 0.375 0.389 0.444
Cumulative control rate 0.727 0.750 0.833
Stage-wise test statistic -1.536 -1.799 -2.567
Stage-wise p-value 0.0623 0.0360 0.0051
Inverse normal combination 1.536 2.358 3.407
Test action continue reject and stop reject and stop
Conditional rejection probability 0.0806 0.3181 0.9110
94.81% repeated confidence interval [-0.737; 0.194] [-0.644; 0.000] [-0.617; -0.142]
Repeated p-value 0.1561 0.0259 0.0009
Final p-value 0.0144
Final confidence interval [-0.656; -0.041]
Median unbiased estimate -0.354

Check RCI

getAnalysisResults(
  design = designIN,
  dataInput = dataExample, 
  thetaH0 = 0.0025,  #  output is rounded!
  directionUpper = FALSE
) |> summary()

Analysis results for a binary endpoint

Sequential analysis with 4 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a two-sample test for rates, normal approximation test. H0: pi(1) - pi(2) = 0.0025 against H1: pi(1) - pi(2) < 0.0025.

Stage 1 2 3 4
Fixed weight 0.5 0.5 0.5 0.5
Cumulative alpha spent 0.0070 0.0138 0.0198 0.0250
Stage levels (one-sided) 0.0070 0.0088 0.0100 0.0110
Efficacy boundary (z-value scale) 2.456 2.372 2.325 2.291
Cumulative effect size -0.352 -0.361 -0.389
Cumulative treatment rate 0.375 0.389 0.444
Cumulative control rate 0.727 0.750 0.833
Stage-wise test statistic -1.547 -1.811 -2.577
Stage-wise p-value 0.0610 0.0351 0.0050
Inverse normal combination 1.547 2.374 3.427
Test action continue reject and stop reject and stop
Conditional rejection probability 0.0790 0.3170 0.9118
95% repeated confidence interval [-0.739; 0.197] [-0.646; 0.002] [-0.618; -0.140]
Repeated p-value 0.1534 0.0249 0.0008
Final p-value 0.0138
Final confidence interval [-0.658; -0.039]
Median unbiased estimate -0.354

Comparison of point estimates

results <- getAnalysisResults(
  design = designIN,
  dataInput = dataExample, 
  thetaH0 = 0.0025,  
  directionUpper = FALSE
)

results$.stageResults$effectSizes
[1] -0.3522727 -0.3611111 -0.3888889         NA
results$medianUnbiasedEstimates
[1]         NA -0.3538987         NA         NA
(results$repeatedConfidenceIntervalLowerBounds + results$repeatedConfidenceIntervalUpperBounds) / 2 
[1] -0.2706451 -0.3216712 -0.3794755         NA

Testing means

dataExample <- getDataset(
  n     = c(28, 40,  29),
  means = c(0.33, 0.42, 0.37), 
  stDevs = c(0.97, 0.93, 0.88)
)

results <- getAnalysisResults(
  design = designIN,
  dataInput = dataExample 
)

summary(results)

Testing means

Analysis results for a continuous endpoint

Sequential analysis with 4 looks (inverse normal combination test design), one-sided overall significance level 2.5%. The results were calculated using a one-sample t-test. H0: mu = 0 against H1: mu > 0.

Stage 1 2 3 4
Fixed weight 0.5 0.5 0.5 0.5
Cumulative alpha spent 0.0070 0.0138 0.0198 0.0250
Stage levels (one-sided) 0.0070 0.0088 0.0100 0.0110
Efficacy boundary (z-value scale) 2.456 2.372 2.325 2.291
Cumulative effect size 0.330 0.383 0.379
Cumulative standard deviation 0.970 0.941 0.918
Stage-wise test statistic 1.800 2.856 2.264
Stage-wise p-value 0.0415 0.0034 0.0157
Inverse normal combination 1.733 3.138 3.804
Test action continue reject and stop reject and stop
Conditional rejection probability 0.1040 0.7069 0.9776
95% repeated confidence interval [-0.151; 0.811] [0.097; 0.662] [0.152; 0.601]
Repeated p-value 0.1120 0.0028 0.0002
Final p-value 0.0075
Final confidence interval [0.077; 0.577]
Median unbiased estimate 0.342 
results$.stageResults$effectSizes
[1] 0.3300000 0.3829412 0.3790722        NA
results$medianUnbiasedEstimates
[1]        NA 0.3422945        NA        NA
(results$repeatedConfidenceIntervalLowerBounds + results$repeatedConfidenceIntervalUpperBounds) / 2 
[1] 0.3300000 0.3799040 0.3766444        NA

Covariate Adjusted Analysis

Introduction

  • Compute adjusted means and estimated standard deviations for continuous outcomes in a two-armed trial with covariates.

  • Perform group sequential test with adjusted p-values from ANCOVA.

  • Use the function getDataset() as an utility function to process adjusted means and estimated standard deviations from raw data.

  • This is done through the extraction of lm coefficients from the specified ANCOVA.

Analysis of raw data – Data import from csv file

Artificial dataset that was randomly generated with simulated normal data.
The dataset has six variables:

  1. Subject id
  2. Stage number
  3. Group name
  4. An example outcome in that we are interested in
  5. The first covariate gender
  6. The second covariate covariate

data <- read.csv(file = "files/data_two_arm_adjusted_means.csv")

data
    subject stage           group    outcome gender covariate
1      1101     1 Treatment group  60.915332      m  41.74395
2      1102     1 Treatment group  57.651981      f  43.94315
3      1103     1 Treatment group 118.367548      f  38.82385
4      1104     1 Treatment group 118.251238      m  36.79198
5      1105     1 Treatment group 174.353213      f  42.92030
6      1106     1 Treatment group 113.806819      f  36.30031
7      1107     1 Treatment group  48.692310      m  38.79058
8      1108     1 Treatment group 120.793274      f  41.98949
9      1109     1 Treatment group 102.074481      m  43.56432
10     1110     1 Treatment group  66.653356      m  41.28624
11     1111     1 Treatment group 192.789917      m  33.28636
12     1112     1 Treatment group  96.103188      f  46.12874
13     1113     1 Treatment group 175.411482      m  45.50095
14     1114     1 Treatment group 179.898767      m  33.24516
15     1115     1 Treatment group  64.836731      f  41.73938
16     1116     1 Treatment group 138.559278      m  45.31195
17     1117     1 Treatment group  29.529644      m  35.75133
18     1118     1 Treatment group 122.545254      f  42.96523
19     1119     1 Treatment group 128.296674      f  44.73482
20     1120     1 Treatment group 110.110602      f  44.49367
21     1121     1 Treatment group  45.991520      f  33.88518
22     1122     1 Treatment group  87.296190      m  36.73631
23     1123     1 Treatment group  92.254379      f  38.08448
24     1124     1 Treatment group  96.479000      f  41.33588
25     1125     1 Treatment group  97.732579      m  44.31532
26     1126     1 Treatment group  63.020381      m  38.82376
27     1127     1 Treatment group 236.277237      f  41.20683
28     1128     1 Treatment group         NA      m  42.33282
29     1129     1 Treatment group  45.273090      m  43.90040
30     1130     1 Treatment group  56.091711      m  39.27349
31     1131     1 Treatment group 134.051026      f  39.04124
32     1132     1 Treatment group  97.138590      f  44.51122
33     1133     1 Treatment group 106.926291      m  34.70051
34     1134     1 Treatment group  68.084850      m  38.63797
35     1135     1 Treatment group 135.710674      m  35.48387
36     1136     1 Treatment group 172.006534      m  43.41109
37     1137     1 Treatment group  79.420273      f  52.92393
38     1138     1 Treatment group  88.884478      m  39.24610
39     1139     1 Treatment group  72.875501      m  43.17024
40     1140     1 Treatment group  62.499853      m  35.90245
41     1141     1 Treatment group 112.013073      m  35.75578
42     1142     1 Treatment group 108.973606      f  37.57677
43     1143     1 Treatment group         NA      f  38.43325
44     1144     1 Treatment group 108.609868      m  44.35666
45     1145     1 Treatment group 196.333999      f  42.28084
46     1146     1 Treatment group  95.173415      f  39.94827
47     1147     1 Treatment group  31.068515      m  40.39852
48     1148     1 Treatment group         NA      f  37.29137
49     1149     1 Treatment group  84.588106      f  42.04340
50     1150     1 Treatment group 128.541775      m  44.99807
51     1151     1 Treatment group 118.149249      m  40.69396
52     1152     1 Treatment group 108.698464      m  45.93401
53     1153     1 Treatment group  66.551613      m  39.51589
54     1154     1 Treatment group  66.795196      m  37.24943
55     1155     1 Treatment group 148.194515      f  41.63981
56     1156     1 Treatment group  97.581556      m  43.30963
57     1157     1 Treatment group  87.086105      f  44.24383
58     1158     1 Treatment group  75.265103      m  48.30317
59     1159     1 Treatment group 115.077812      f  44.97853
60     1160     1 Treatment group 215.990333      m  37.98066
61     1161     1 Treatment group  83.430914      f  37.53304
62     1162     1 Treatment group 133.453484      f  33.68154
63     1163     1 Treatment group 139.787199      f  41.92989
64     1164     1 Treatment group 189.090864      m  47.64797
65     1165     1 Treatment group  96.461852      f  34.88215
66     1166     1 Treatment group 149.629258      m  34.87189
67     1167     1 Treatment group  87.983660      m  37.79579
68     1168     1 Treatment group 125.487429      f  39.74570
69     1169     1 Treatment group  49.868054      f  40.15935
70     1170     1 Treatment group 111.678537      m  41.74537
71     1171     1 Treatment group 155.733073      m  37.03043
72     1172     1 Treatment group  89.898656      f  38.49887
73     1173     1 Treatment group 133.281809      m  38.02761
74     1174     1 Treatment group 180.787879      f  37.27137
75     1175     1 Treatment group 181.326264      f  42.22095
76     1176     1 Treatment group  46.644730      f  34.46649
77     1177     1 Treatment group 182.160889      m  44.23738
78     1178     1 Treatment group 235.734964      f  44.07047
79     1179     1 Treatment group 123.596910      f  39.80186
80     1180     1 Treatment group 100.572744      f  31.83763
81     1181     1 Treatment group  79.068517      m  39.61799
82     1182     1 Treatment group 119.959232      m  39.33848
83     1183     1 Treatment group  79.618169      m  42.26236
84     1184     1 Treatment group 101.267554      f  38.10153
85     1185     1 Treatment group  85.285744      m  43.76071
86     1186     1 Treatment group 125.969216      m  37.75873
87     1187     1 Treatment group 104.409242      m  46.81732
88     1201     1   Control group 118.111978      f  46.37750
89     1202     1   Control group 112.803047      f  50.56341
90     1203     1   Control group 106.279228      m  46.16517
91     1204     1   Control group  26.137107      m  55.66513
92     1205     1   Control group 121.703709      m  46.10107
93     1206     1   Control group  28.179089      f  47.32115
94     1207     1   Control group 166.258299      m  50.56693
95     1208     1   Control group  93.908330      m  48.99593
96     1209     1   Control group 117.873985      f  44.74084
97     1210     1   Control group  77.797407      m  51.11756
98     1211     1   Control group  97.793048      f  45.79823
99     1212     1   Control group  34.490830      f  47.80869
100    1213     1   Control group 108.603770      m  55.23996
101    1214     1   Control group  80.016652      f  54.73093
102    1215     1   Control group 180.938509      m  49.60275
103    1216     1   Control group 119.506045      f  48.43063
104    1217     1   Control group 130.953498      m  45.92114
105    1218     1   Control group -51.531817      f  49.71211
106    1219     1   Control group 140.740705      f  46.09804
107    1220     1   Control group  83.788848      f  57.85032
108    1221     1   Control group  73.960984      m  51.60963
109    1222     1   Control group  41.871488      m  44.46589
110    1223     1   Control group  87.101741      m  48.91804
111    1224     1   Control group  21.869485      m  54.32146
112    1225     1   Control group 130.166118      f  45.12141
113    1226     1   Control group 123.082088      m  50.82517
114    1227     1   Control group 142.370876      f  46.80575
115    1228     1   Control group  65.328749      f  56.64114
116    1229     1   Control group 118.455944      f  48.18142
117    1230     1   Control group 141.864325      m  48.35794
118    1231     1   Control group  74.501536      f  54.57813
119    1232     1   Control group  41.971384      m  44.73958
120    1233     1   Control group 114.503414      f  46.72186
121    1234     1   Control group 166.778918      f  53.91904
122    1235     1   Control group 107.779407      m  48.52357
123    1236     1   Control group 141.209154      f  53.76970
124    1237     1   Control group  85.258166      m  49.97739
125    1238     1   Control group 123.324872      f  58.23043
126    1239     1   Control group 106.191564      m  48.04120
127    1240     1   Control group 136.704361      f  49.95438
128    1241     1   Control group 168.320594      f  49.83972
129    1242     1   Control group 191.833899      f  44.82796
130    1243     1   Control group  41.993953      f  47.82318
131    1244     1   Control group 122.223310      m  51.26559
132    1245     1   Control group 107.417838      f  41.08096
133    1246     1   Control group  66.660155      f  44.16594
134    1247     1   Control group 118.630493      f  49.50234
135    1248     1   Control group 103.357250      m  50.14601
136    1249     1   Control group  68.091491      m  47.21945
137    1250     1   Control group 197.232504      m  52.14219
138    1251     1   Control group  55.352899      f  52.05785
139    1252     1   Control group  95.254020      f  55.60368
140    1253     1   Control group  84.331326      f  45.64885
141    1254     1   Control group  55.833782      m  49.94821
142    1255     1   Control group -25.137811      m  54.53565
143    1256     1   Control group  58.127828      f  59.07245
144    1257     1   Control group  62.478912      m  56.62178
145    1258     1   Control group 106.973422      f  44.66975
146    1259     1   Control group 110.471942      f  56.09414
147    1260     1   Control group 113.071582      m  54.36411
148    1261     1   Control group  64.365801      m  44.54071
149    1262     1   Control group  88.582148      m  51.48605
150    1263     1   Control group 108.000380      f  48.18828
151    1264     1   Control group 107.973560      f  49.99834
152    1265     1   Control group  19.778149      f  50.24998
153    1266     1   Control group 181.203995      f  50.44074
154    1267     1   Control group 144.530158      f  48.07444
155    1268     1   Control group 138.653984      f  45.89275
156    1269     1   Control group -13.645824      f  46.27012
157    1270     1   Control group  70.376653      f  54.58227
158    1271     1   Control group  79.519125      f  49.23130
159    1272     1   Control group  23.968025      f  50.48166
160    1273     1   Control group 146.145097      f  47.41035
161    1274     1   Control group  75.505468      m  54.12894
162    1275     1   Control group  64.769655      m  51.41633
163    1276     1   Control group  44.061803      m  50.83071
164    1277     1   Control group  62.239958      m  56.12589
165    1278     1   Control group  96.003713      m  51.44122
166    1279     1   Control group 158.426362      m  43.78677
167    1280     1   Control group  28.771248      m  50.45153
168    1281     1   Control group  75.185158      f  51.54136
169    1282     1   Control group -27.140455      m  51.43388
170    1283     1   Control group  74.475666      m  50.67419
171    1284     1   Control group 103.817718      m  45.48959
172    1285     1   Control group  61.775227      m  56.85924
173    1286     1   Control group 114.031613      m  44.89346
174    1287     1   Control group  42.393840      m  52.27747
175    2101     2 Treatment group 148.131778      m  33.76559
176    2102     2 Treatment group  96.019897      f  40.68627
177    2103     2 Treatment group         NA      f  43.29108
178    2104     2 Treatment group         NA      m  39.47415
179    2105     2 Treatment group 124.068427      f  41.29759
180    2106     2 Treatment group 226.969836      m  41.12901
181    2107     2 Treatment group 123.405054      m  43.50771
182    2108     2 Treatment group         NA      m  37.00055
183    2109     2 Treatment group 101.649519      m  41.92557
184    2110     2 Treatment group 152.672985      m  36.02520
185    2111     2 Treatment group 129.906677      m  46.45029
186    2112     2 Treatment group 101.838703      m  35.06772
187    2113     2 Treatment group  69.199847      f  36.18072
188    2114     2 Treatment group 185.983430      m  38.82010
189    2115     2 Treatment group  54.855420      m  41.00171
190    2116     2 Treatment group 195.816339      f  44.44986
191    2117     2 Treatment group 148.873317      m  43.99352
192    2118     2 Treatment group  73.546096      f  38.59094
193    2119     2 Treatment group 131.324795      m  41.23274
194    2120     2 Treatment group  70.147824      m  41.09979
195    2121     2 Treatment group 165.142632      m  38.58412
196    2122     2 Treatment group  63.119932      m  43.86155
197    2123     2 Treatment group 113.534704      m  40.48399
198    2124     2 Treatment group  56.760798      m  41.35577
199    2125     2 Treatment group 113.147409      m  43.40006
200    2126     2 Treatment group 161.692264      f  41.28116
201    2127     2 Treatment group         NA      m  38.61404
202    2128     2 Treatment group 144.895706      m  40.52785
203    2129     2 Treatment group 120.076608      m  40.93657
204    2130     2 Treatment group 167.198650      m  37.69830
205    2131     2 Treatment group  92.370218      f  42.38907
206    2132     2 Treatment group 174.970652      f  42.71503
207    2133     2 Treatment group  43.700108      f  36.92546
208    2134     2 Treatment group  86.721918      f  38.58603
209    2135     2 Treatment group 173.329034      m  36.65433
210    2136     2 Treatment group  68.955282      m  46.10965
211    2137     2 Treatment group -13.494525      m  44.82764
212    2138     2 Treatment group -12.219344      m  45.74248
213    2139     2 Treatment group  93.200749      f  33.26283
214    2140     2 Treatment group 127.781442      f  41.19897
215    2141     2 Treatment group  99.416015      m  39.88825
216    2142     2 Treatment group  83.291346      f  40.62557
217    2143     2 Treatment group 104.417974      f  35.15310
218    2144     2 Treatment group  53.158243      m  43.69736
219    2145     2 Treatment group 131.279052      m  37.56266
220    2146     2 Treatment group 146.385221      f  46.89227
221    2147     2 Treatment group  87.871764      m  41.71479
222    2148     2 Treatment group  92.074664      f  36.69945
223    2149     2 Treatment group 145.358484      f  37.25947
224    2150     2 Treatment group 127.476922      f  42.75383
225    2151     2 Treatment group  87.122459      f  36.80236
226    2152     2 Treatment group  99.468734      m  40.72832
227    2153     2 Treatment group 116.205793      m  45.07193
228    2154     2 Treatment group 118.363383      m  36.11800
229    2155     2 Treatment group 195.779889      m  46.85061
230    2156     2 Treatment group  84.809065      f  34.89991
231    2157     2 Treatment group 122.554800      m  37.26509
232    2158     2 Treatment group  40.524856      f  40.69914
233    2159     2 Treatment group  75.646884      m  37.54613
234    2160     2 Treatment group 129.848641      m  41.91331
235    2161     2 Treatment group 159.660881      f  42.99501
236    2162     2 Treatment group  85.972244      f  36.97553
237    2163     2 Treatment group  54.394505      f  40.09344
238    2164     2 Treatment group 152.676684      f  41.60451
239    2165     2 Treatment group 149.225960      f  48.85437
240    2166     2 Treatment group 169.240155      f  37.02340
241    2167     2 Treatment group 155.218245      m  39.26598
242    2168     2 Treatment group         NA      f  31.72879
243    2169     2 Treatment group 102.263295      m  45.52036
244    2170     2 Treatment group 223.272314      m  36.12225
245    2171     2 Treatment group 161.310825      f  37.35040
246    2172     2 Treatment group  66.869670      f  41.80688
247    2173     2 Treatment group 188.059613      f  40.23286
248    2174     2 Treatment group 121.116022      m  39.61774
249    2175     2 Treatment group  64.347836      f  36.83015
250    2176     2 Treatment group 114.101965      f  31.02810
251    2177     2 Treatment group         NA      m  38.26138
252    2178     2 Treatment group  67.757731      m  42.71542
253    2179     2 Treatment group 131.464220      f  36.02921
254    2180     2 Treatment group  53.728041      m  42.26535
255    2181     2 Treatment group 207.710614      f  37.34099
256    2182     2 Treatment group  98.115872      f  41.14550
257    2183     2 Treatment group 146.508829      m  40.63603
258    2184     2 Treatment group         NA      f  37.68016
259    2185     2 Treatment group         NA      f  46.09672
260    2186     2 Treatment group  33.627667      m  34.10929
261    2187     2 Treatment group  88.514103      m  36.74357
262    2201     2   Control group  85.564947      f  48.77833
263    2202     2   Control group  88.082937      f  54.62074
264    2203     2   Control group 101.821924      m  47.39312
265    2204     2   Control group  69.498987      f  52.80377
266    2205     2   Control group  76.389332      f  58.28917
267    2206     2   Control group 197.718320      f  42.83755
268    2207     2   Control group  80.491819      f  52.43532
269    2208     2   Control group  88.790640      m  52.52622
270    2209     2   Control group  27.785576      f  56.67482
271    2210     2   Control group 110.395608      f  43.89054
272    2211     2   Control group 189.602362      f  55.32527
273    2212     2   Control group 116.706192      f  55.56885
274    2213     2   Control group  53.403402      m  47.87397
275    2214     2   Control group  92.197839      m  44.35599
276    2215     2   Control group 226.719523      m  48.81198
277    2216     2   Control group  84.333440      f  52.99306
278    2217     2   Control group 115.058642      m  54.70769
279    2218     2   Control group         NA      m  46.39091
280    2219     2   Control group 147.045933      f  44.11154
281    2220     2   Control group 145.633095      m  47.38888
282    2221     2   Control group 109.577890      m  52.24456
283    2222     2   Control group  78.273341      m  51.52679
284    2223     2   Control group 134.503543      f  54.62293
285    2224     2   Control group  94.809806      f  47.20078
286    2225     2   Control group 135.254918      f  50.73824
287    2226     2   Control group 148.096839      f  45.33651
288    2227     2   Control group 145.754822      m  52.73534
289    2228     2   Control group  98.575321      f  49.67044
290    2229     2   Control group  84.415325      f  57.12815
291    2230     2   Control group 102.888916      m  57.98899
292    2231     2   Control group 140.332164      f  55.65008
293    2232     2   Control group   8.320178      m  47.40147
294    2233     2   Control group 125.140663      f  53.81962
295    2234     2   Control group  54.703761      m  51.37802
296    2235     2   Control group  46.116927      f  51.06964
297    2236     2   Control group  92.555462      f  51.79276
298    2237     2   Control group  14.522516      m  48.26737
299    2238     2   Control group 100.949270      m  49.60221
300    2239     2   Control group  79.767910      m  49.06210
301    2240     2   Control group  90.308179      m  51.51113
302    2241     2   Control group 122.417868      f  49.19103
303    2242     2   Control group 125.701298      f  43.04404
304    2243     2   Control group  80.288039      m  48.82796
305    2244     2   Control group         NA      m  49.91225
306    2245     2   Control group  72.630434      f  48.91357
307    2246     2   Control group 115.662673      f  46.31431
308    2247     2   Control group 109.296894      f  54.15588
309    2248     2   Control group 165.928627      m  49.03998
310    2249     2   Control group 170.922467      f  52.29195
311    2250     2   Control group  58.384495      f  51.25386
312    2251     2   Control group  73.276353      f  45.32873
313    2252     2   Control group 140.114730      m  47.54660
314    2253     2   Control group  99.767996      f  55.15153
315    2254     2   Control group  83.453778      m  47.17067
316    2255     2   Control group  55.070047      f  48.32911
317    2256     2   Control group 137.944829      f  46.83519
318    2257     2   Control group 148.862366      f  45.56954
319    2258     2   Control group 192.977651      f  46.47892
320    2259     2   Control group         NA      f  47.55053
321    2260     2   Control group 126.582645      f  45.94865
322    2261     2   Control group  49.077900      m  54.33169
323    2262     2   Control group 133.681737      f  54.85075
324    2263     2   Control group         NA      m  49.64795
325    2264     2   Control group 142.001442      f  53.00226
326    2265     2   Control group  56.745110      f  57.85307
327    2266     2   Control group  96.816275      m  47.72682
328    2267     2   Control group  61.024866      f  53.09593
329    2268     2   Control group 150.454543      m  48.96315
330    2269     2   Control group         NA      m  47.66897
331    2270     2   Control group  26.374563      m  47.95530
332    2271     2   Control group 125.200981      f  45.77897
333    2272     2   Control group  48.343088      f  49.53677
334    2273     2   Control group 109.939541      m  50.17042
335    2274     2   Control group 121.184452      m  43.51048
336    2275     2   Control group  70.503523      f  43.82258
337    2276     2   Control group  72.173708      m  54.43203
338    2277     2   Control group 121.700156      f  46.58076
339    2278     2   Control group 156.618216      m  50.78377
340    2279     2   Control group 104.218127      m  55.62978
341    2280     2   Control group  95.432526      f  50.75085
342    2281     2   Control group  80.111379      f  49.03208
343    2282     2   Control group  80.764990      m  47.83391
344    2283     2   Control group  85.959962      f  45.98712
345    2284     2   Control group  57.806390      m  49.90178
346    2285     2   Control group  49.848225      m  47.97988
347    2286     2   Control group  82.906745      m  36.75354
348    2287     2   Control group 110.143634      m  53.83601
349    3101     3 Treatment group         NA      f  37.05855
350    3102     3 Treatment group 132.686821      m  35.38209
351    3103     3 Treatment group 116.465935      m  40.54073
352    3104     3 Treatment group  66.917001      f  40.46552
353    3105     3 Treatment group  47.367119      f  30.74220
354    3106     3 Treatment group  58.379236      f  37.44284
355    3107     3 Treatment group 110.739491      f  35.89004
356    3108     3 Treatment group  81.081427      m  40.40304
357    3109     3 Treatment group  52.659663      f  38.27292
358    3110     3 Treatment group 137.259307      f  38.31598
359    3111     3 Treatment group 153.571282      f  43.47181
360    3112     3 Treatment group  42.974304      m  41.27459
361    3113     3 Treatment group 166.359787      m  40.43385
362    3114     3 Treatment group 110.927051      f  39.70792
363    3115     3 Treatment group 154.557347      f  44.44999
364    3116     3 Treatment group 152.931023      m  37.41464
365    3117     3 Treatment group 176.262379      f  45.19103
366    3118     3 Treatment group 134.657888      f  33.57611
367    3119     3 Treatment group 139.546056      f  44.05511
368    3120     3 Treatment group 108.655997      m  49.86927
369    3121     3 Treatment group 146.394313      f  33.15128
370    3122     3 Treatment group 149.523079      m  39.85511
371    3123     3 Treatment group         NA      f  47.91566
372    3124     3 Treatment group 111.001226      m  36.62415
373    3125     3 Treatment group 137.601642      m  41.86731
374    3126     3 Treatment group 154.712589      m  40.07737
375    3127     3 Treatment group         NA      m  36.62378
376    3128     3 Treatment group  57.389282      m  37.46763
377    3129     3 Treatment group 112.487959      f  41.81212
378    3130     3 Treatment group  72.250398      m  39.89877
379    3131     3 Treatment group  74.116637      f  33.12508
380    3132     3 Treatment group 112.939898      m  47.62506
381    3133     3 Treatment group 111.476979      m  37.99934
382    3134     3 Treatment group 131.728488      f  38.57493
383    3135     3 Treatment group  83.194743      f  42.18571
384    3136     3 Treatment group 104.394697      f  39.89532
385    3137     3 Treatment group  99.983298      m  52.23134
386    3138     3 Treatment group 174.189731      m  37.86288
387    3139     3 Treatment group 150.213645      m  38.37308
388    3140     3 Treatment group 111.278931      m  42.90348
389    3141     3 Treatment group 155.235685      m  39.23105
390    3142     3 Treatment group         NA      m  39.85354
391    3143     3 Treatment group  19.168745      m  42.65444
392    3144     3 Treatment group  84.300096      f  47.29241
393    3145     3 Treatment group 102.904584      m  41.95029
394    3146     3 Treatment group 164.233127      f  35.85762
395    3147     3 Treatment group 136.038318      m  39.70299
396    3148     3 Treatment group 153.309155      f  40.15767
397    3149     3 Treatment group 127.137619      f  32.14231
398    3150     3 Treatment group 125.723040      f  34.88946
399    3151     3 Treatment group         NA      m  44.69287
400    3152     3 Treatment group  31.703569      f  37.78620
401    3153     3 Treatment group  92.051807      f  43.79473
402    3154     3 Treatment group  61.988920      m  42.64916
403    3155     3 Treatment group 113.898607      m  38.97650
404    3156     3 Treatment group  73.991145      f  37.26279
405    3157     3 Treatment group 134.495540      f  36.23496
406    3158     3 Treatment group  72.868983      f  38.29469
407    3159     3 Treatment group 123.198132      m  43.90163
408    3160     3 Treatment group 173.338378      f  42.33495
409    3161     3 Treatment group  51.372879      m  47.56015
410    3162     3 Treatment group 172.311821      m  40.49924
411    3163     3 Treatment group  80.200637      m  48.45671
412    3164     3 Treatment group 135.886550      f  43.11422
413    3165     3 Treatment group 171.772277      f  40.20925
414    3166     3 Treatment group  86.930035      m  32.69204
415    3167     3 Treatment group  71.560094      m  38.89218
416    3168     3 Treatment group  73.478903      f  41.15659
417    3169     3 Treatment group 115.108725      m  37.03049
418    3170     3 Treatment group 112.103818      m  44.42098
419    3171     3 Treatment group 124.067430      m  40.61990
420    3172     3 Treatment group  74.694741      m  38.35915
421    3173     3 Treatment group 190.573973      m  43.32773
422    3174     3 Treatment group 122.778944      m  39.90866
423    3175     3 Treatment group  37.885741      m  42.15401
424    3176     3 Treatment group  44.499568      m  37.58959
425    3177     3 Treatment group  92.811917      f  47.34769
426    3178     3 Treatment group 140.987541      f  47.09875
427    3179     3 Treatment group 135.592114      m  37.43826
428    3180     3 Treatment group  94.638832      f  34.25275
429    3181     3 Treatment group 157.434538      m  37.72336
430    3182     3 Treatment group  85.191469      f  40.55705
431    3183     3 Treatment group         NA      f  35.11954
432    3184     3 Treatment group  96.350144      m  33.44092
433    3185     3 Treatment group 165.367348      f  32.15146
434    3186     3 Treatment group 126.834457      f  46.39305
435    3187     3 Treatment group 141.352334      f  38.98428
436    3201     3   Control group  34.832079      m  56.24827
437    3202     3   Control group  96.555220      f  41.13241
438    3203     3   Control group 136.665569      f  57.55534
439    3204     3   Control group 135.408417      m  52.08284
440    3205     3   Control group 124.148072      m  48.27186
441    3206     3   Control group 148.716103      m  45.74130
442    3207     3   Control group 156.474217      m  55.13459
443    3208     3   Control group 124.338738      f  45.24798
444    3209     3   Control group 113.045544      m  47.24965
445    3210     3   Control group  67.325378      m  58.15828
446    3211     3   Control group 151.936579      m  48.19020
447    3212     3   Control group  48.274224      m  51.62957
448    3213     3   Control group 110.921896      m  42.53740
449    3214     3   Control group         NA      m  47.32559
450    3215     3   Control group  78.694529      m  46.89681
451    3216     3   Control group 118.783075      f  46.36409
452    3217     3   Control group 113.346049      m  51.39292
453    3218     3   Control group  94.800393      f  54.89816
454    3219     3   Control group 104.624253      f  53.53600
455    3220     3   Control group  79.130211      m  49.75042
456    3221     3   Control group 131.894370      m  52.79761
457    3222     3   Control group  95.670441      f  43.17321
458    3223     3   Control group 158.759474      f  47.04224
459    3224     3   Control group 159.733150      m  50.52292
460    3225     3   Control group  84.536571      f  56.66061
461    3226     3   Control group 129.206365      f  51.80294
462    3227     3   Control group 106.178744      m  53.65963
463    3228     3   Control group  95.339266      m  44.20129
464    3229     3   Control group  44.132266      f  52.31818
465    3230     3   Control group 165.814366      m  53.02770
466    3231     3   Control group 156.416520      m  56.68947
467    3232     3   Control group 113.566511      f  49.53512
468    3233     3   Control group 101.553866      f  58.62003
469    3234     3   Control group  76.063126      m  51.65975
470    3235     3   Control group  78.502634      f  51.45126
471    3236     3   Control group 138.362305      f  43.01998
472    3237     3   Control group  95.515339      f  47.61101
473    3238     3   Control group 150.061546      m  56.10989
474    3239     3   Control group  78.789239      m  55.47055
475    3240     3   Control group  64.233677      f  51.54327
476    3241     3   Control group         NA      f  54.03477
477    3242     3   Control group 148.275732      m  50.83201
478    3243     3   Control group  55.585295      f  44.52878
479    3244     3   Control group 127.634854      f  50.28173
480    3245     3   Control group 124.594417      f  49.27128
481    3246     3   Control group  90.869787      f  47.82496
482    3247     3   Control group 112.821896      m  50.01732
483    3248     3   Control group  37.847365      f  45.59440
484    3249     3   Control group 139.773020      f  48.88853
485    3250     3   Control group  64.465354      f  44.76273
486    3251     3   Control group  78.734330      f  44.63858
487    3252     3   Control group  77.291938      m  49.21485
488    3253     3   Control group 140.221457      m  58.05126
489    3254     3   Control group  56.251883      f  49.77089
490    3255     3   Control group  98.050236      f  53.86956
491    3256     3   Control group 101.893805      m  45.79153
492    3257     3   Control group 132.814488      f  49.22607
493    3258     3   Control group  61.003921      f  52.15981
494    3259     3   Control group         NA      m  47.93062
495    3260     3   Control group 214.093571      m  55.05460
496    3261     3   Control group 175.266404      m  54.09582
497    3262     3   Control group  97.911617      m  46.80821
498    3263     3   Control group 103.177106      m  49.22286
499    3264     3   Control group 104.514201      m  51.58350
500    3265     3   Control group  42.777349      m  51.36250
501    3266     3   Control group  53.693940      m  52.85972
502    3267     3   Control group  89.049355      f  51.12560
503    3268     3   Control group  84.684626      f  48.38651
504    3269     3   Control group 123.106424      m  54.44183
505    3270     3   Control group 105.301444      f  52.85300
506    3271     3   Control group  81.151131      f  48.15543
507    3272     3   Control group  73.293516      f  55.23280
508    3273     3   Control group 165.100800      m  52.89296
509    3274     3   Control group  29.577311      m  52.07602
510    3275     3   Control group 116.156177      f  52.18838
511    3276     3   Control group  69.961762      f  46.87931
512    3277     3   Control group  60.536586      f  53.21085
513    3278     3   Control group  84.347802      m  49.99937
514    3279     3   Control group  64.247337      m  46.20406
515    3280     3   Control group 112.674026      f  52.04577
516    3281     3   Control group 128.883116      f  53.70692
517    3282     3   Control group  49.807103      f  53.62298
518    3283     3   Control group 115.903755      m  49.53783
519    3284     3   Control group 171.430741      f  49.07528
520    3285     3   Control group  79.466659      m  50.97486
521    3286     3   Control group 120.677498      f  47.32595
522    3287     3   Control group  51.209303      f  48.79702

Analysis of raw data – Descriptive Statistics

means <- aggregate(x = data$outcome, by = list(data$group,
    data$stage), FUN = mean, na.rm = TRUE)
stDevs <- aggregate(x = data$outcome, by = list(data$group,
    data$stage), FUN = sd, na.rm = TRUE)
sampleSizes <- aggregate(x = na.omit(data)$outcome, by = list(na.omit(data)$group,
    na.omit(data)$stage), FUN = length)

tab <- data.frame(stage = means$Group.2,
                    arm = means$Group.1,
                    n = sampleSizes$x,
                    mean = means$x,
                    std = stDevs$x
                  ) |> print()
  stage             arm  n      mean      std
1     1   Control group 87  91.66591 49.13310
2     1 Treatment group 84 110.88731 45.65258
3     2   Control group 82 101.83443 41.97826
4     2 Treatment group 79 114.06969 49.06744
5     3   Control group 84 103.31525 37.87368
6     3 Treatment group 81 112.17591 39.91061

The mean of outcome is larger in the treatment group as in the control group.

Interim analysis Stage 1

Create a group sequential design with default parameters:

library(rpact)
design <- getDesignGroupSequential()
summary(design)

Sequential analysis with a maximum of 3 looks (group sequential design)

O’Brien & Fleming design, one-sided overall significance level 2.5%, power 80%, undefined endpoint, inflation factor 1.0174, ASN H1 0.8562, ASN H01 0.9831, ASN H0 1.0149.

Stage 1 2 3
Planned information rate 33.3% 66.7% 100%
Cumulative alpha spent 0.0003 0.0072 0.0250
Stage levels (one-sided) 0.0003 0.0071 0.0225
Efficacy boundary (z-value scale) 3.471 2.454 2.004
Cumulative power 0.0329 0.4424 0.8000

Overall p-values should be compared with stage levels


Select stage 1 data

data1 <- data[data$stage == 1, ]

Then create a linear model with dependent variable y = outcome, independent variable group, and covariates covariate and gender, i.e., the model formula is outcome ~ group + covariate + gender:

lmResult1 <- lm(
  outcome ~ group + covariate + gender, 
  data = data1
)
summary(lmResult1)

Call:
lm(formula = outcome ~ group + covariate + gender, data = data1)

Residuals:
     Min       1Q   Median       3Q      Max 
-148.504  -26.561   -0.007   25.211  122.130 

Coefficients:
                     Estimate Std. Error t value Pr(>|t|)   
(Intercept)          139.2393    46.1660   3.016  0.00296 **
groupTreatment group  11.8357    11.3411   1.044  0.29817   
covariate             -0.8502     0.9174  -0.927  0.35540   
genderm              -10.5387     7.2567  -1.452  0.14830   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 47.31 on 167 degrees of freedom
  (3 Beobachtungen als fehlend gelöscht)
Multiple R-squared:  0.057, Adjusted R-squared:  0.04006 
F-statistic: 3.365 on 3 and 167 DF,  p-value: 0.02006

Extract the adjusted effects and standard deviations from the lmResult1 object:

cat("coefficients = ", summary(lmResult1)$coefficients[2, ], "\n")
coefficients =  11.83574 11.34113 1.043612 0.2981733


Create rpact data set

  effect <- summary(lmResult1)$coefficients[2, 1]
  stErr <- summary(lmResult1)$coefficients[2, 2]
  sampleSizes <- aggregate(x = na.omit(data1)$outcome, by = list(na.omit(data1)$group), FUN = length)
  stDev <- stErr / sqrt(1/sampleSizes$x[1] + 1/sampleSizes$x[2])

  rpactDataset <- getDataset(
    cumMeans1 = effect,
    cumMeans2 = 0,
    cumStDevs1 = stDev,
    cumStDevs2 = stDev,
    cumN1 = sampleSizes$x[1],
    cumN2 = sampleSizes$x[2]
  )

Perform analysis

  getAnalysisResults(
    design = design,
    dataInput = rpactDataset
    ) |> summary()

Analysis results for a continuous endpoint

Sequential analysis with 3 looks (group sequential design), one-sided overall significance level 2.5%. The results were calculated using a two-sample t-test, equal variances option. H0: mu(1) - mu(2) = 0 against H1: mu(1) - mu(2) > 0.

Stage 1 2 3
Planned information rate 33.3% 66.7% 100%
Cumulative alpha spent 0.0003 0.0072 0.0250
Stage levels (one-sided) 0.0003 0.0071 0.0225
Efficacy boundary (z-value scale) 3.471 2.454 2.004
Cumulative effect size 11.836
Cumulative (pooled) standard deviation 74.141
Overall test statistic 1.044
Overall p-value 0.1491
Test action continue
Conditional rejection probability 0.0457
95% repeated confidence interval [-28.304; 51.975]
Repeated p-value 0.3668 

  x <- getAnalysisResults(
    design = design,
    dataInput = rpactDataset
    ) 
  x$.stageResults$effectSizes
[1] 11.83574       NA       NA
  x$.stageResults$overallTestStatistics
[1] 1.043612       NA       NA
  2*(x$.stageResults$overallPValues)
[1] 0.2981555        NA        NA

Do it over all three stages

data <- read.csv(file = "files/data_two_arm_adjusted_means.csv")

Then use the function unique to identify the available stages in the data.frame:

stages <- sort(
  as.integer(unique(data$stage))
)

as.integer ensures that the stages will be valid also if data$stage is a factor.

Loop over all stages and calculate the adjusted means and standard deviations

effects <- rep(0, length(stages))
stDevs <- rep(0, length(stages))
sampleSizes1 <- rep(0, length(stages))
sampleSizes2 <- rep(0, length(stages))
for (stage in stages){
  dataSet <- data[data$stage <= stage, ]
  lmResult <- lm(
    outcome ~ group + covariate + gender,
    data = dataSet
  )
  cat("stage = ", stage, summary(lmResult)$coefficients[2, ], "\n")
  effect <- summary(lmResult)$coefficients[2, 1]
  stErr <- summary(lmResult)$coefficients[2, 2]
  sampleSizes <- aggregate(x = na.omit(dataSet)$outcome, by = list(na.omit(dataSet)$group), FUN = length)
  stDev <- stErr / sqrt(1/sampleSizes$x[1] + 1/sampleSizes$x[2])

  effects[stage] <- effect
  stDevs[stage] <- stDev
  sampleSizes1[stage]<- sampleSizes$x[1]
  sampleSizes2[stage]<- sampleSizes$x[2]
}
stage =  1 11.83574 11.34113 1.043612 0.2981733 
stage =  2 8.418143 8.139495 1.034234 0.3017887 
stage =  3 10.1669 6.377269 1.594241 0.111523 
rpactDataset <- getDataset(
  cumMeans1 = effects,
  cumMeans2 = rep(0, length(stages)),
  cumStDevs1 = stDevs,
  cumStDevs2 = stDevs,
  cumN1 = sampleSizes1,
  cumN2 = sampleSizes2
)

Perform analysis

getAnalysisResults(
  design = design,
  dataInput = rpactDataset
) |> summary()

Perform analysis

Analysis results for a continuous endpoint

Sequential analysis with 3 looks (group sequential design), one-sided overall significance level 2.5%. The results were calculated using a two-sample t-test, equal variances option. H0: mu(1) - mu(2) = 0 against H1: mu(1) - mu(2) > 0.

Stage 1 2 3
Planned information rate 33.3% 66.7% 100%
Cumulative alpha spent 0.0003 0.0072 0.0250
Stage levels (one-sided) 0.0003 0.0071 0.0225
Efficacy boundary (z-value scale) 3.471 2.454 2.004
Cumulative effect size 11.836 8.418 10.167
Cumulative (pooled) standard deviation 74.141 74.142 71.074
Overall test statistic 1.044 1.034 1.594
Overall p-value 0.1491 0.1509 0.0558
Test action continue continue accept
Conditional rejection probability 0.0457 0.0222
95% repeated confidence interval [-28.304; 51.975] [-11.667; 28.503] [-2.646; 22.980]
Repeated p-value 0.3668 0.2584 0.0648
Final p-value 0.0568
Final confidence interval [-2.416; 22.622]
Median unbiased estimate 10.111